Propagating Errors for Experiment 1 3 4 e g GR ρ π Formula for density. 2 Propagation of Error In many experimental lab courses you learn a rather mysterious-looking formula for the error bars of derived or calculated quantities.

Summary Of Rules For Error Propagation
Propagation equation is correct as far as it goes small errors linear approximations etc it is often not true that the resulting uncertainty has a Gaussian distribution.

Exact formula for propagation of error. Sometimes the measurement of interest cannot be replicated directly and it is necessary to estimate its uncertainty via propagation of error formulas. 2 31 3 44gRe ee g ρ GR GR σ σσ ππ Take partial derivatives and add errors in quadrature g Re gRe σσρ σ ρ. Is called its standard error.
If we had multiplied the numbers together instead of adding them our result would have been 032 according to the rules of significant figures. X n Figure 3. SV pR2s L p2 cm3.
Equation 9 is of the form with 10. N Using propagation of errors. Error propagation in a multi-input single-output system.
Nn P 1 X1 X2 X3 Xn System Y YfX 1X 2. The total differential is then. Error Propagation Suppose that we make N observations of a quantity x that is subject to random fluctuations or measurement errors.
The previous post demonstrates the effect of the measurement errors that can creep in if you are predicting the period using the given formula T 2πlg. Recall that X has mean µ and variance σ2n so it has standard deviation σ n. In other words the absolute.
Rewriting Equation 7 using the statistical relationship created yields the Exact Formula for Propagation of Error. 9 σ x 2 δ x δ a 2 σ a 2 δ x δ b 2 σ b 2 δ x δ c 2 σ c 2. In this article we shall study the propagation of errors in different mathematical operations like addition subtraction multiplication and division and.
According to the rules for propagation of error the result of our calculation is 1513 001 exactly what the significant figure rules gave us. The general method of getting formulas for propagating errors involves the total differential of a function. δT T 1 2 δl l δg g which is the formula for error propagation concerning T or.
N Let R 1 cm exact and L 10 05 cm. I just discovered this amazing online resource. Exact error calculated analytically.
The general formula for the propagation of errors is then 𝑅𝑅 2 2𝑅 2 2 where 𝑅 is the notation for the partial derivative. The distribution of is therefore Gaussian and we have to determine and. Equation 9 shows a direct statistical relationship between multiple variables and their standard deviations.
The purpose of these measurements is to determine q which is a function of x1xn. V p p2 cm3. X n is any function of x ix i1.
δT T 2 δl l δg g Answer link. Suppose that z fw x y where the variables w x y etc. µ q xn xn 2 10501 8.
The main tool for getting at standard errors is the central limit theorem. L Unphysical situations can arise if we use the propagation of errors results blindlyu Example. T Let t 3004 days k 00547day-1 and A 0 123x10 3s.
Equation 6 can be written as f f s a x x 2 b y y 2 8 which indeed is much simpler to use than equation 6. I can calculate the standard error of Y by error-propagation as sY 1m sqrt sm²A-Bm² sA² sB² Now I want to get a confidence interval for Y so I need the degrees of. General Formula for Error Propagation Wemeasure x1x2xn withuncertainties x1x2xn.
If the result 𝑅 is a function of measurements where 𝑅. Suppose we measure the volume of a cylinder. Must be independent variables.
This is when you compare the size of your error to the size of the original quantity1 The formula for relative error is. It seems to agree with the way of thinking that has been provided in this note but it takes you through it all through graphs an pictures instead of jokes and text. Log a bpow c2sin c with variables a b c.
Thus the end result is achieved. 11 As in chapter 21 the approximation is linear. If qqx ix i1.
Summary-propagation of errors General formula for propagation of error. Error Propagation tutorialdoc Daley 5 10909 A tA 0 ekt where A t is the activity at time t A 0 is the initial activity and k is the decay constant. Our best estimate of the true value for this quantity is then êxês x where êêx 1 ÅÅÅÅÅÅÅ N i1 N xi sx 2 1 ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ N-1 i1 N Hxi-êêxL2 are the sample mean and variance.
RelX X jXj 1 Thus in the above example your 1cm uncertainty on your 589m measure-ment would turn into a relative error of 00016. The propagation of error formula for Y. The uncertainty in q is then q sµ q x1 x1 2.
N If the error on V sV is to be interpreted in the Gaussian sense. 12 13 14 15 16 17 18 19 20 YfX 1X 2. Assuming a negligible error in A 0 and k the uncertainty in the activity is determined by any uncertainty in the time.
X n then Provided all errors are independent and random 31. A t A t k. Error calculated by this tool numerically.

Summary Of Rules For Error Propagation
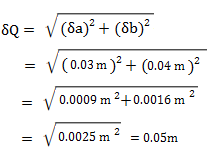
Error Propagation Propagation Of Uncertainty Statistics How To
Error Propagation Calculator Online Tool For Any Formula